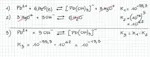Barbara
2017-04-27 19:23
Buonasera,
Nonostante numerosi tentativi ancora non sono riuscita a risolvere il seguente esercizio:
"La costante di equilibrio della reazione
Pb2+(aq) + 6H2O(l) ⇄ Pb(OH)3-(aq) + 3H3O+(aq)
è 10^-55,3.
Calcolare la costante di equilibrio della reazione:
Pb2+(aq) + 3OH-(aq) ⇄ Pb(OH)3- (aq) "
La soluzione ufficiale è 10 elevato alla -13,3.
Come tentativo di risoluzione ho scritto la formula necessaria per ricavare entrambe le costanti di equilibrio.
[H3O+]^3 [Pb(OH)3-]
K=----------------------------- = 10^-55,3
[Pb2+] [H2O]^6
[Pb(OH)3-]
K=-----------------------= X
[OH]^3 [Pb2+]
Ho anche pensato che forse sarebbe utile considerare che la concentrazione molare dell'acqua nell'acqua stessa è di 55,5 moli per litro oppure che si potrebbe considerare scomporre in ione idronio e ossidrile.
Tuttavia non sono riuscita a pervenire ad un risultato o perlomeno non a quello esatto.
Scusate per la grafia non troppo corretta delle reazione e delle formule, ma non sono riuscita ad utilizzare né gli apici né i pedici.
Ringrazio in anticipo chi sarà così gentile e disponibile da rispondere al mio quesito.
Barbara