Luigi
2019-06-05 20:42
Luigi
2019-06-05 20:42
Ciao a tutti 
Volevo chiedere se qualcuno sapesse dimostrare come mai calore e lavoro non sono due grandezze di stato.
Ho postato in questa discussione perché non sapevo dove altrimenti, non mi sembrava da "esercizi", poiché più una richiesta di tipo teorico...
FLaCaTa100
2019-06-06 05:53
Calore e lavoro non sono due funzioni di stato in quanto dipendono dal modo in cui è avvenuta la trasformazione e dal percorso che ha fatto. Se ci pensi il lavoro è l'area sottesa dalla curva in un grafico F vs spostamento, se fissi i punti di partenza e di arrivo ma cambi la curva, l'integrale assumerà sempre valori differenti. Ciò significa che il lavoro non dipende solo dallo stato finale e quello iniziale ma anche da come ci si arriva.
I seguenti utenti ringraziano FLaCaTa100 per questo messaggio: Luigi, luigi_67
Luigi
2019-06-06 05:59
So la definizione di funzione di stato e so bene che queste due grandezze non lo sono... ma se volessi dimostrare questo con conoscenze termodinamiche come potrei farlo?
thenicktm
2019-06-17 10:09
Come ti è già stato spiegato lavoro e calore non sono funzioni di stato, ma andiamo ad analizzarle dal punto di vista matematico e termodinamico come da te chiesto.
Partiamo da alcune nozioni di base di Analisi Matematica II per arrivare al nocciolo della risposta. I seguenti argomenti saranno tuttavia riassuntivi e invito per chi volesse approfondire i differenziali di studiarli in proprio dalla moltitudine di link e video-corsi disponibili sul web.
Il Primo principio della termodinamica rappresenta una formulazione più generale della legge di conservazione dell’energia; esso fu formulato nel XIX secolo perché prevede l’interpretazione del calore come forma di energia.
Da ricordare che:
Dal punto di vista matematico il lavoro e il calore non sono invece in generale funzioni di stato, poiché essi non ammettono un differenziale esatto, quindi dipendono dalla natura della trasformazione.
Per capire meglio il concetto sono essenziali alcuni richiami di Analisi Matematica, reperibili on-line che metto a vostra disposizione.
Consideriamo una variabile x;
Un'espressione avente forma:
è detta forma differenziale. Evidentemente dQ "sbarrato", così come dx, dy e dz sono differenziali ed esiste una relazione funzionale tra di essi.
Le precedenti forme differenziali sono dette esatte se esiste una funzione Q = f(x), Q = f(x,y), Q = f(x,y,z) che, nei 3 casi proposti, soddisfa rispettivamente le condizioni:
Non è detto che la funzione f esista, eccetto nel caso di una forma differenziale in una sola variabile.
In generale, pertanto, non è detto che il differenziale dQ sia un differenziale esatto. Indichiamo i differenziali non-esatti con la lettera d barrata: d. Per esempio: dQ, dL, ecc. (Alcuni libri di testo indicano i differenziali non esatti con δ)
La forma differenziale dQ = A(x)dx è sempre esatta, perchè si può trovare una funzione f tale che:

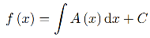
Consideriamo ora la forma differenziale: dQ = A(x,y)dx +B(x,y)dy
Per poterla scrivere nella forma esatta: 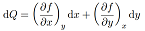
sarebbe necessario trovare una funzione f (x, y) tale che: 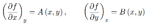
Queste condizioni sono verificate soltanto nel caso particolarissimo nel quale, tra le funzioni A(x,y) e B(x,y), sussista la relazione: 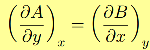
Alcuni esempi:
Un sistema termodinamico è descritto da un certo numero di parametri termodinamici (temperatura, volume, pressione, ecc.). Il numero di parametri necessario a descrivere il sistema è la dimensione dello spazio di stato del sistema (D).
In questo esempio, il sistema è specificato in modo univoco da due parametri come pressione e volume, oppure pressione e temperatura. Queste scelte sono equivalenti: sono solo differenti sistemi di coordinate nello spazio termodinamico bidimensionale. Un ragionamento analogo vale per gli spazi dimensionali a dimensione maggiore.
Mentre il sistema cambia il proprio stato, descrive un "percorso" nello spazio degli stati. Questo percorso può essere identificato attraverso i valori che assumono le funzioni di stato durante la trasformazione in funzione del tempo o di qualche altra variabile esterna.
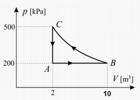
Il lavoro per andare da C a B non è lo stesso se compiuto lungo l'isoterma o lungo la successione isocora-isobara. Vediamo perchè:
Caso della trasformazione isocora: 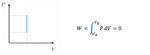
Caso della trasformazione isobara: 
Caso della trasformazione isoterma: 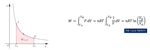
Riassumendo:
Lungo l'isoterma: W = nRT ln(Vb/Vc)
Lungo isocora+isobara: W = 0 + nRTb(1-Va/Vb)
Il lavoro totale è diverso nei due casi: dipende dal percorso seguito e non può essere scritto come una variazione di una funzione di stato.
Ora, con alcuni passaggi matematici si può dimostrare che il Volume nell'equazione di stato dei gas perfetti compare sotto forma di funzione di stato, mentre il lavoro delle forze di pressione dipende, come visto dal grafico precedente, dal percorso seguito, come osservato precedentemente.
Considerando infatti V= nRT/P si può calcolare la variazione del volume del gas da uno stato iniziale ad uno stato finale:
Per il Teorema di Schwarz possiamo prima far variare la pressione da Pi a Pf mantenendo la temperatura costante e pari a Ti quindi la temperatura da Ti a Tf mantenendo la pressione costante e pari a Pf. Utilizzando l'equazione di stato:
Il differenziale è esatto, poichè:
Le due derivate parziali miste seconde sono uguali e quindi il differenziale è esatto.
Come già detto, al contrario del volume, il lavoro dipende dal percorso seguito e il lavoro svolto durante la trasformazione infinitesimale dW non è un differenziale esatto.
Allego uno dei tanti link che spiega e dimostra quanto detto precedentemente per il concetto di Lavoro quì
Le stesse considerazioni possono essere fatte sul calore che è strettamente connesso al concetto di temperatura. Il calore fluisce dai punti a temperatura maggiore a quelli a temperatura minore, finché non viene raggiunto l'equilibrio termico. Il quantitativo di calore scambiato dipende dal particolare percorso seguito dalla trasformazione per arrivare dallo stato iniziale allo stato finale, così come il lavoro.
Per qualsiasi chiarimento o segnalazione di eventuali errori resto a disposizione nel limite nelle mie conoscenze 
Fonti: Appunti di Fisica Generale I, Analisi matematica II, Termodinamica
Fonti dal web: https://it.wikipedia.org/wiki/CaloreCalore, https://it.wikipedia.org/wiki/Funzione_di_statoFunzione di stato, https://www.chimica-online.it/download/funzioni-di-stato.htmFunzione di stato 2, http://significatofisico.blogspot.com/2011/11/variabili-e-funzioni-termodinamiche_9.htmlVariabili e funzioni termodinamiche, http://significatofisico.blogspot.com/2011/11/un-differenziale-esatto_17.htmlDifferenziale esatto, http://significatofisico.blogspot.com/2011/11/il-lavoro-di-volume_23.htmlLavoro di volume, https://www.youmath.it/forum/analisi-2n/39422-teorema-di-schwartz.htmlTeorema di Schwarz
I seguenti utenti ringraziano thenicktm per questo messaggio: Luigi, Hamiltoniano, A.Berenini, Claudio, Mercaptano, myttex
Mercaptano
2021-10-30 18:45
Mi permetto di aggiungere, rileggendo la magnifica risposta di thenicktm, che l'applicazione del teorema di Schwartz è fondamentale anche in altre applicazioni ai potenziali termodinamici, ad esempio è alla base delle relazioni di Maxwell.
Da un punto di vista puramente matematico, invece, perché possiamo applicare il teorema bisogna che le derivate parziali miste (o almeno una delle derivate parziali miste) siano continue nell'intervallo di definizione. In caso contrario non possiamo dire nulla a priori e ci tocca calcolare a mano queste derivate per ogni combinazione possibile.
I seguenti utenti ringraziano Mercaptano per questo messaggio: thenicktm