Chemistry4888
2012-03-16 16:00
Salve,
dopo un periodo super incasinato fra tesi, ritorno in portogallo e burocrazia universitaria riprendo ad ampliare questa sezione del forum. Finalmente siamo arrivati a trattare la costruzione della matrice z di una molecola da inserire all'interno del file di input.
Prima di tutto bisogna dire che per costruire la matrice Z, ci sono due metodi principali, il primo adotta l'uso di software appositi ( ad esempio ChemOffice) il secondo sfrutta le conoscenze chimiche di base dell'operatore e tanta pazienza. 
Naturalmente tratteremo entrambi i metodi per dare l'opportunità a tutti di costruire una matrice Z. Inutile dirvi che il metodo più utilizzato è quello che sfrutta il pacchetto ChemOffice.
Metodo Computerizzato
Questo metodo sfrutta due programmi presenti nel pachetto ChemOffice, ChemDraw e Chem3D. Gli step per la costruzione della matrice Z (o anche cartesiana se uno preferisce) attraverso questo metodo sono molto semplici e sono riportati di seguito:
- Aprire ChemDraw
- Disegnare la molecola al ChemDraw
- Copiare la molecola del ChemDraw
- Aprire Chem3D
- Incollare la molecola precedentemente copiata
- Selezionare dal menù di Chem3D: Visualizza matrice e scegliere Matrice Z o Matrice Cartesiana Copiare la matrice e allegarla al file Input
Davvero semplicissimo, in pochi istanti avrete la vostra molecola pronta per essere inserita nel file Input, senza aver speso un minimo di energia. 
Metodo non computerizzato
Passiamo ora a vedere il metodo non computerizzato, non molto utilizzato ma in caso di necessità può tornare utile. In questo caso non è possibile ottenere la matrice cartesiana del sistema (sarebbe possibile ma il procedimento è molto complesso e noioso) ma solamente la matrice Z.
La matrice Z esprime la geometria della molecola sotto forma di matrice. Non l'avreste mai detto vero?  .
.
Iniziamo a vedere come si costruisce.
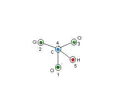
Per prima cosa bisogna disegnare la nostra molecola su un foglio di carta e in seguito numerare (in maniera assolutamente soggettiva) ogni atomo che comprende la molecola. Di seguito posto un piccolo esempio per la molecola dell'etano sfalzato (Fig.1).
Fig.1 Esempio di numerazione per la molecola dell'etano sfalzato
Adesso bisogna descrivere la posizione degli atomi, presenti nella molecola osservando la numerazione prescritta in precedenza. Per prima cosa dovremmo descrive l'atomo 1, che consiste nell'origine del nostro sistema (nel piano cartesiano corrisponde al punto 0,0,0). Per descrivere l'origine basta scrivere l'elemento di appartenenza e il corrispondente numero. Nel nostro caso la prima riga della matrice Z per la molecola dell'etano sarà:
H1 Davvero semplicissimo 
Passiamo ora a descrivere la posizione del secondo atomo del nostro sistema, riferendoci naturalmente all'origine scelta. Come si possono definire due punti in uno spazio conoscendo la posizione di uno di loro?
La cosa più banale è definire la distanza fra essi (non è sufficiente ma descrivendo gli atomi successivi il programma ottiene tutte le informazioni per descrivere la posizione dell'atomo 2). Naturalmente bisogna definire l'atomo desiderato (nel nostro caso il 2), l'atomo di riferimento ( nel nostro caso H1) e la distanza fra essi (la distanza di un generico legame C-H è di 1.09 amstrong). Quindi sapendo queste informazioni possiamo scrivere la seconda riga della nostra matrice:
C2 (atomo descritto) 1 (atomo di riferimento) 1.09 (distanza fra essi)
Fra un informazione e un altra bisogna sempre lasciare uno spazio (meglio con il TAB che con la barra spaziatrice) altrimenti il programma non riesce ad interpretare la matrice descritta. Inoltre qualsiasi valore inserito nella matrice deve contenere il punto (1.09, 1. o 1.0). Il punto è essenziale per una corretta lettura da parte di Gaussian.
Stupide Macchine 
Adesso passiamo a definire il terzo atomo (C3) della nostra serie. Come definire un terzo atomo conoscendo la "posizione" dei primi due? Cosa sempre molto banale, attraverso la distanza dal secondo atomo e l'angolo descritto con il primo. Ottimo, non è difficile no!
La procedura da seguire è sempre la stessa, atomo di riferimento e corrispondente valore. In questo caso però dobbiamo definire la distanza di 3 da 2 e l'angolo fra 3 e 1. Distanza di un generico C-C è 1.55 amstrong mentre l'angolo di un sistema tetraedrico è 109.5°. Scriviamo quindi la nostra terza riga della matrice che sarà:
C3 (atomo da descrivere) 2 (atomo di riferimento per la distanza) 1.55 (valore della distanza) 1 (atomo di riferimento per l'angolo) 109.5 (valore dell'angolo)
Gaussian interpreta questo linguaggio (atomo di riferimento e valore associato) fino a un massimo di 3 valori che corrispondono alla distanza in amstrong (primo valore dato), all'angolo in gradi (secondo valore dato) e all'angolo diedro sempre in gradi (terzo valore dato). Attraverso l'associazione di queste informazioni, Gaussian riesce a comprendere la posizione esatta di ogni atomo, in qunato ci sarà solo una geometria associata a quel sistema che corrisponda a quelle determinate distanze, angoli e angoli diedri fra i vari atomi.
Detto questo, per comprendere meglio il pensiero "contorno" (quasi malato) di Gaussian, continuiamo a descrivere il nostro sistema.
Dobbiamo descrivere l'atomo 4 (H4), come fare? La risposta è: attraverso l'angolo diedro. Infatti l'atomo 4, avrà una determinata distanza con il 3, un determinato angolo con il 2 e un determinato angolo diedro con l'1. La distanza di un generico legame C-H è sempre 1.09 amstrong, l'angolo di un sistema tetraedrico è sempre 109.5 mentre l'angolo dietro con l'atomo 1 è 180 gradi, guardare la Fig.1 può aiutare molto (conoscere la definizione di angolo diedro può farlo maggiormente  ).
).
Detto questo, scriviamo la nostra quarta riga della matrice che corrisponde all'atamo H4 che sarà:
H4 (Atomo descritto) 3 (Riferimento 1) 1.09 (Valore 1) 2 (Riferimento 2) 109.5 (Valore 2) 1 (Riferimento 3) 180. (Valore 3)
Naturalmente il riferimento e valore 1, sono per la distanza, il riferimento e valore 2 per l'angolo e infine il riferimento e valore 3 sono per l'angolo diedro.
Una volta scritte le prime 4 righe della matrice (permettono a Gaussian di ottenere le informazione sulla posizione del sistema), possiamo descrivere tutti gli altri atomi della molecola attraverso lo stesso metodo e gli stessi parametri, quindi ad esempio l'atomo 5 (H5) sarà:
H5 (Atomo descritto) 4 (Riferimento 1) 1.09 (Valore 1) 3 (Riferimento 2) 109.5 (Valore 2) 1 (Riferimento 3) 60. (Valore 3)
Se effetuiamo la stessa procedura per i restanti atomi del nostro sistema (H6, H7 ed H8), otteniamo la matrice z che descrive la geometria dell'etano sfalzato. La matrice completa dell'etano sfalzato quindi si presenterà così scritta:
H1
C2 1 1.1
C3 2 1.55 1 109.5
H4 3 1.1 2 109.5 1 180.
H5 3 1.1 2 109.5 1 60.
H6 3 1.1 2 109.5 1 -60.
H7 2 1.1 3 109.5 4 -60.
H8 2 1.1 3 109.5 4 60.
Spero di essere stato chiaro e che abbiate compreso come costruire una matrice Z per una generica molecoal, in caso contrario chiedete chiedete chiedete chiedete. Dubbi e chiarimenti sono ben accetti.
Stay computational 
I seguenti utenti ringraziano Chemistry4888 per questo messaggio: al-ham-bic


 Modifico subito
Modifico subito