Salve 
Ho un dubbio abbastanza stupido ma che mi infastidisce parecchio.
In pratica sul mio libro di studio (chimica inorganica-atkins) nel prima capitolo in cui si parla della struttura atomica e in particolare delle funzioni d'onda che descrivono gli orbitali atomici c'è uno di quei classici e famosi grafici in cui viene mostrata la parte radiale della funzione d'onda R=psi(r) per gli orbitali 1s,2s,3s in funzione del raggio (distanza dal nucleo)
ora non capisco perchè in ASCISSA invece del raggio r trovo scritto così: Raggio, Zr/a_o
dove a_o = raggio di bohr, che è una costante.
In ordinata trovo invece scritto R/(Z/a_o ) tutto elevato a 3/2.
Cioè in genere in ascissa si riporta l'incognita,la variabile indipendente da cui la funzione dipende...
Ma non dovrebbe essere semplicemente r ? perche c'è Zr/a_o ? per un certo atomo non Z e raggi odi bohr non dovrebbero essere costanti?
Grazie!!
Credo dipenda dal fatto che si parli di atomi idrogenoidi e non di idrogeno con Z=1.
grazie "Clorato di sodio" .
Volevo chiedere un'altra cosetta sulla funzione d'onda (o meglio sul quadrato) ma prima devo imparare la scrittura latex mi sa ...
beh provo a scrivere senza scrittura latex perche ancora non sono riuscito a guardare il tutorial... se comunque non si capisce allora
Sempre a riguardo della funzione d'onda il libro dice che Psi(r,alpha,phi)^2 equivale alla densità di probabilità di trovare l'elettrone nel punto di coordinate (r,alpha,phi).
E fin qui tutto ok, direi.
Ora so che è possibile compiere un ulteriore passaggio dicendo che la funzione d'onda può essere scomposta nel prodotto di due funzioni:
psi(r,alpha,phi)=R(r ) * Y(alpha,phi)
CIò permette in linea teorica di separare le variabili e considerare,ad esempio,come varia la densità di probabilità quando a variare è solo la parte radiale o viceversa...
Ora mi è venuto in mente una cosa:
Visto che il quadrato della parte radiale R^2 fornisce la densità di probabilità di trovare l'elettrone a una distanza r dal nucleo, a prescindere dalla direzione è possibile descrivere in prima analisi l'orbitale "s" e come varia la densità elettronica solo con la parte radiale?
Mi sembra abbastanza corretto fare ciò perchè se uno ci pensa l'orbitale "s" ha simmetria sferica e perciò la densità di probabilità di trovare un elettrone a una certa distanza r è la stessa qualunque sia la direzione.
Mi viene da pensare che quindi sempre per l'orbitale "s" la parte angolare sia una costante.
Discorso diverso per l'orbitale "p" dove una descrizione della densità di probabilità attraverso la sola parte radiale non è corretta: ciò è evidente se uno pensa alla sua forma: NON è infatti vero che qualunque punto che si trova in una qualsiasi direzione a una comune distanza "r" ha la stessa densità di probabilità(per l'orbitale p la densità è maggiore lungo l'asse internucleare)...
quindi dal momento che ciò non è vero mi aspetto che la parte angolare assuma in questo caso un ruolo fondamentale nella descrizione esatta della densità di probabilità associata all'orbitale atomico "p" (anche da un semplice punto di vita qualitativo)...e sempre poichè non tutti i punti che sono alla stessa distanza r hanno la stessa densità di probabilità (cosa che invece afferma la sola parte radiale R^2) allora è necessario che la parte angolare non sia più una costante come nel caso dell'orbitale "s"....
Volevo sapere se queste supposizioni sono esatte: supposizioni fatte basandosi solo sulla forma dell'orbitale atomico( che poi altro non è che tutti i punti dello spazio in cui la densità di probabilità elettronica è maggiore di una certa soglia) senza scomodare la meccanica quantistica.
Cioè per un orbitale atomico "s" la parte radiale mi pare fornisca già una descrizione qualitativa sufficiente sulla densità elettronica ( la parte angolare essendo una costante,modificherà tutti i valori assunti dalla parte radiale di una semplice costante comune).
Cosa diversa per l'orbitale "p" in cui osservando la forma si intuisce che la funzione radiale non possa descrivere correttamente l'orbitale ma anzi sia necessaria anche la parte angolare (non piu una costante) che tiene conto anche della direzionalità modulando i valori della parte radiale in modo che si abbia alla fine la forma classica dell'orbitale atomico...
CHe ne pensate?
Spero di aver scritto nel modo più chiaro possibile.
Grazie!!
Diciamo che l'esame di chimica fisica I era tanto tempo fa, ora come ora di parti radiali e angolari ricordo ben poco.
Proverò a documentarmi e vedrò di risponderti!
NaClO3 ha scritto:
Diciamo che l'esame di chimica fisica I era tanto tempo fa, ora come ora di parti radiali e angolari ricordo ben poco.
Proverò a documentarmi e vedrò di risponderti!
no vabbè...se ti interessa riguardartela per curiosità è un conto, ma se devi "perdere tempo" per risolvere questa mia curiosità/dubbio lascia pure perdere  Tanto tra un po' dovrò iniziare a studiare per l'esame di chimica-fisica2 che sarà solo su ste cose: funzione d'onda,equazione di schrodinger,teoria dei gruppi e spettroscopia...
Sono argomenti molto interessanti ma allo stesso tempo abbastanza complessi se li si vuole capire a fondo.
Tanto tra un po' dovrò iniziare a studiare per l'esame di chimica-fisica2 che sarà solo su ste cose: funzione d'onda,equazione di schrodinger,teoria dei gruppi e spettroscopia...
Sono argomenti molto interessanti ma allo stesso tempo abbastanza complessi se li si vuole capire a fondo.
Axeldt95
2015-04-03 15:40
xshadow ha scritto:
Ora so che è possibile compiere un ulteriore passaggio dicendo che la funzione d'onda può essere scomposta nel prodotto di due funzioni:
psi(r,alpha,phi)=R( r ) * Y(alpha,phi)
Ciò permette in linea teorica di separare le variabili e considerare,ad esempio,come varia la densità di probabilità quando a variare è solo la parte radiale o viceversa...
Ora mi è venuto in mente una cosa:
Visto che il quadrato della parte radiale R^2 fornisce la densità di probabilità di trovare l'elettrone a una distanza r dal nucleo, a prescindere dalla direzione è possibile descrivere in prima analisi l'orbitale "s" e come varia la densità elettronica solo con la parte radiale?
La generica equazione =R(%20r%20)Y(\alpha,\phi)) per gli orbitali atomici di tipo s diventa
per gli orbitali atomici di tipo s diventa =R_{n,0}(%20r%20)Y_{0,0}(\alpha,\phi)) .
.
Risolvendo l'equazione relativa alla funzione d'onda angolare si ottiene 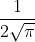 , dunque quel termine della funzione d'onda non è dipendente da
, dunque quel termine della funzione d'onda non è dipendente da 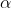 e da
e da 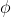 diversamente da ciò che accade quando il numero quantico angolare è maggiore di 0.
diversamente da ciò che accade quando il numero quantico angolare è maggiore di 0.
La funzione d'onda assumerà la forma =\frac{1}{2\sqrt{\pi}}R_{n,0}(%20r%20)) che come avevi ipotizzato dipende solamente da r.
che come avevi ipotizzato dipende solamente da r.
Axeldt95 ha scritto:
La generica equazione =R(%20r%20)Y(\alpha,\phi)) per gli orbitali atomici di tipo s diventa
per gli orbitali atomici di tipo s diventa =R_{n,0}(%20r%20)Y_{0,0}(\alpha,\phi)) .
.
Risolvendo l'equazione relativa alla funzione d'onda angolare si ottiene 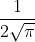 , dunque quel termine della funzione d'onda non è dipendente da
, dunque quel termine della funzione d'onda non è dipendente da 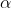 e da
e da 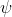 diversamente da ciò che accade quando il numero quantico angolare è maggiore di 0.
diversamente da ciò che accade quando il numero quantico angolare è maggiore di 0.
La funzione d'onda assumerà la forma =\frac{1}{2\sqrt{\pi}}R_{n,0}(%20r%20)) che come avevi ipotizzato dipende solamente da r.
che come avevi ipotizzato dipende solamente da r.
grazie mille per l'accurata descrizione  !!
!!
sto iniziando a studiare chimica fisica 2 e quindi queste cose sperò le capirò bene...
però nel frattempo volevo giusto farmi un'idea sull'argomento...ed effettivamente anche senza concetti troppo difficili ma facendo giusto un paio di collegamenti è possibile trarre già alcune conclusioni qualitative.
